１） イントロダクション
資産運用について考えるとき、運用の評価は欠かせない手続きの一つです。これから投資をしようというとき、どの投資対象がどれぐらい好ましいかは、誰もが最初に考えることの一つでしょう。また、投資戦略をたて、それを実行し、投資期間の途中や終わりに、自分が選んだ投資戦略が果たして成功したか、ということは、誰にとっても興味深いことです。以下では、こうした投資一般について考えるとき、どのようにその評価を行うべきかについて、順を追って説明します。なお、算数の使用はできるだけ避けたいと思います。算数は嫌いだという方もおられるからです。しかし、ことがお金儲けに関わる以上、計算するという手続きは評価に欠かせませんので、こうした算数の部分は付録にまとめてあります。
２）トータル・リターン
投資評価の基本は、
a) いくら投資して、
b) いくら回収したのか、
この2つが基本です。しかし、もう少し詳しく見ると、
c) いつ投資して、いつ回収したのか
という問題が含まれていることがわかります。次のような投資を考えましょう。100万円を投資して、1年後に20万円、2年後に110万円回収したとします。この収益を測るとき、単純に1年後に受け取った20万円を、2年後に受け取った110万円と合計しては、2年後だけに130万円を受け取ったケースと区別がつきません。そこで、1年後に受け取った20万円は、その時の価格で、元の資産に再投資したと仮定し、2年後には合計でいくらの資産になっているか、ということを考えます。
単純化のために、1年後に20万円の分配金を支払った後、その資産の価格は100万円に戻っていたとすれば、それが更に1年後には110万円になったわけですから、1年後に受け取った20万円は2年後には20×(110÷100) = 22万円になっているはずです。したがって、2年後には合計110+22 = 132万円受け取っている計算になります。こうしておいて、2年後だけに130万円を受け取ったケースと比べれば、前者の方が2年後の資産額が2万円だけ大きく、よりよい投資であったといえそうです。こうした、投資期間中に発生したキャッシュフローを全て再投資していれば投資期間終了時に全額まとめていくらになっていたかでパフォーマンスを測る考え方を、トータル・リターンといいます。トータル・リターンは、同じ投資期間で、同じような投資対象同士を比べるときに便利な道具です。
また、投資期間が同じ投資対象同士ならば、収益額ではなく収益率で比較することも可能です。上記の前者のケースならば、トータル・リターンは金額ベースで32万円、収益率ベースで32÷100 = 32%です。こうして、投資金額に対して何%の収益率であったかを考えることで、価格の違う資産同士の比較が簡単に行えます。例えば、1000円の株式が1100円になった場合と、100円の株式が160円になった場合を比べると、収益金額ベースでは前者の方が大きいですが、「同じだけの金額を投資していたらどうなったか」を考える場合、前者は10%、後者は60%、といった収益率で考えた方がよいでしょう。さらに、通常収益率は複利計算の年率で表示します。最初のケースに戻って、2年間で32%のトータル・リターンを得たならば、複利年率の収益率は、
になります。
３）トータル・リスク
異なる種類の資産や投資のパフォーマンスを比較したり、また比較が可能な形でパフォーマンスを数量化するためには、前項で説明したa) 投資額、b) 回収額、c) 回収タイミングの3つに加え、d) どれぐらいのリスクを伴う投資であるかを考慮する必要があります。真剣に投資を考えるならば、誰でも高いリターンと低いリスクを好みます。リスクが低く、リターンが高い投資は誰の目にも明らかに良い投資ですが、リスクもリターンも低い投資と、リスクもリターンも高い投資を比較する必要がある場合には、2）で説明したようなトータル・リターンの比較では不十分です。リスクが高ければより高いリターンでないと我々は満足しませんし、リスクが低い投資ならばリターンが低くでも満足できる場合があるからです。こうしたとき、トータル・リターンを%で測り、「投資した金額当たりのトータル・リターン」を考えたように、「取ったトータル・リスク当たりのリターン」を考えれば良いでしょう。具体的には、シャープレシオと呼ばれる指標が良く用いられます。
トータルリターンは前項で説明した複利年率のトータルリターン、リスクフリー金利とは、リスクがない投資のトータルリターンで、通常割引国債や短期金融商品の利回りなどが用いられます。また、取ったトータルリスクの大きさは、トータルリターンの標準偏差で測ります。
リスクフリー金利をトータルリターンから差し引くのは、あえてリスクを取らなくても、リスクフリー金利で運用すればいくらかのリターンが得られるからです。これを差し引くことで、あえてリスクを取ったことで、リスクを取らない場合に比べ、より高いリターンがどれだけ得られたかを計算していることになります。これを、「リスクフリー金利に対する超過収益率」と呼びます。この超過収益率をトータルリスクで割ることで、取ったリスク当たりの超過収益率が計算されています。シャープレシオは、1990年のノーベル賞受賞経済学者、ウィリアムシャープが提唱したパフォーマンス評価指標です。この指標は、保有している資産全体や、リスク資産全体のパフォーマンスを評価する場合に適切な指標です。シャープレシオが高いほど、より好ましいパフォーマンスであると言えます。
４）リスク・リターンの分解
前項ではトータルリターンとトータルリスクを考えましたが、一般にリスクとリターンはシステマティックリスク・リターンと、レジデュアルリスク・リターンに分解することができます。システマティックリスク・リターンは、市場全体と連動して発生するリスクとリターンです。つまり、市場全体が上昇するときにそれに連動してどれぐらい大きなリターンが得られるかがシステマティックリターン、また市場全体が上下するとき、それに連動してどれぐらい激しく価格が上下するかがシステマティックリスクです。市場全体と連動して発生するリスクとリターンを考えるのは、それが「誰にでも簡単にとることのできるリスクとリターン」だからです。インデックスファンドを買えば、それだけでシステマティックリスクとシステマティックリターンが得られます。問題になるのは、どれぐらいの大きさでそれらをとるかということだけで、投資しさえすれば、リサーチも、研究も、能力も才能も必要なく、持っているだけでシステマティックなリスクとリターンを得ることができます。「システマティック」とは意訳すれば「自動的な」という意味です。これに対し、レジデュアルリスク・リターンはアクティブ運用特有のリスクとリターンです。レジデュアルとは「残った」とか「残差の」とかといった意味で、システマティックリスク・リターンを取り除いた後に残ったリスクとリターンを指します。
５）システマティックリスク・リターン
システマティックリスクは通常β（ベータ）という指標で表されます。β= 1が市場全体と同程度のシステマティックリスク、β= 0がシステマティックリスク = 0です。例えば、インデックスファンドのβは1ですし、「純資産と同額のインデックス先物を売り建てします」と銘打ったベアファンドのβは-1です。また、インデックスファンドに70%、リスクフリー金利に30%のアセットアロケーションを行えば、その資産全体のβは0.7です。
システマティックリターンは、次のような計算で求められます。
大括弧[ ]の中身は、市場インデックスの「リスクフリー金利に対する超過収益率」です。これにbをかけることで、取ったシステマティックリスクから考えて対リスクフリー金利超過収益率がどれだけ得られているべきかが計算されています。これを、リスクプレミアムと呼びます。最後に、これにリスクフリー金利を足すことで、システマティックリターンが計算できます。
６）レジデュアルリターン
システマティックリターンは、同じぐらいのシステマティックリスクを取れば、ただただインデックスファンドを持っているだけで、リサーチや売買などの手間隙やコストを掛けなくても得られるであろうリターンを示しています。言い換えれば、これぐらいのリターンは、プロを雇わなくてもシステマティックリスクを取りさえすれば誰にでも達成可能だ、というリターンです。これに対し、トータルリターンからこれを差し引いたレジデュアルリターンは、誰にでも労せずして投資が可能なインデックスファンドにあえて投資せず、より高いリターンを求めて積極的な運用を行うことによって得られるリターンです。言い換えれば、このレジデュアルリターンこそは、アクティブ運用の成果をあらわす指標です。レジデュアルリターンはα（アルファ）ともよばれ、次のように計算できます。
インデックスファンドのαは、取引コストや小さな誤差を除けば、0になります。αがプラスの投資は、同じだけのシステマティックリスクを取りさえすれば誰にでもあげられるリターンを上回るリターンを示すので、一般により好ましい成果であると言えます。
なお、こうして計算したαは、全投資家の時価加重平均を取れば必ず0になります。株式を例に取れば、全投資家の保有株式を合計すれば株式市場全体になります。株式市場全体のリターンの時価加重平均は当然市場インデックスですから、全投資家の株式運用の時価加重平均は、市場インデックスと同じ、したがってαは0です。ですから、αは、アクティブ運用者の成果を測るときに用いられます。プラスならうまい運用、マイナスならヘタな運用を行ったといえます。
７）レジデュアルリスク
αが発生するような積極的な運用をするということは、同じだけのシステマティックリスクを取ったインデックスファンドとリスクフリー金利の組み合わせとは異なるリターンの変動=リスクが発生することを意味します。この、システマティックリスクとは無関係に発生するリスクをレジデュアルリスクといいます。リターンの場合はレジデュアルリターン=αは引き算で求めることが出来ましたが、一般にリスクの場合は単純な足し算・引き算でその大きさを計算することはできません。
アクティブ運用にもいろいろな程度があり、人によっては個別株式一本釣りで勝負しますし、別の人はインデックス運用に多少色をつけた程度のアクティブ運用を行います。つまり、人によって取っているレジデュアルリスクの大きさは様々です。投資信託のアクティブ運用担当者も同様です。それならば、これまで説明してきた考え方同様、単純なαではなく、「取ったレジデュアルリスク当たりのレジデュアルリターン」でパフォーマンスを見るべきだと思いませんか?こうしたとき、一般には情報比（IR: information ratio）と呼ばれる指標が使われます。
投資信託の場合ならば、このIRを見ることで、アクティブ運用担当者がどれぐらい効率よく、レジデュアルリスクを取っているかを測ることができます。IRは、スタイルマネジメントなどの方法を使って多数のアクティブ運用者に分散して資金を運用させるとき、有効なパフォーマンス評価測度です。
８）それで?
さて、これまで投資一般のパフォーマンス評価の方法を説明してきましたが、一つ重要なことを議論していません。それは、パフォーマンス評価は何のためにするのか、ということです。一般には、次の2つではないでしょうか。
a) 過去の運用成果について検証する。
b) これから投資をしようというときに、より良い投資対象を選択する。
a)の意味でのパフォーマンス評価は、投資信託の運用会社がファンドマネージャーのボーナスを決めるときに使われますし、また年金基金などの機関投資家が各運用委託先の成績を見るときにも使われます。しかし、個人投資家がパフォーマンス評価を考えるとき、多くの場合その目的はb)であるように思います。では、この目的のために、これまで説明してきた各種のパフォーマンス評価測度は、有効でしょうか?
多くの場合、b)の目的でのパフォーマンス評価も、a)の場合と同じく、過去のデータを用いて行われます。投資信託などの広告や販売用資料、そして投資信託評価機関が与える「星の数」も、過去のパフォーマンスです。この点について、筆者は前から不思議に思っていることがあります。例えば株式や為替なら、最近の（つまり過去の）パフォーマンスを見て単純に順張りで買うか買わないかを決める人は、それほどいません。チャートをやる人は確かに最近の株価の動き、ようするに過去のパフォーマンスを見ますが、彼らも単純に「最近この株は上がっているから、今後も上がるに違いない」という、シンプルな見方はしないようです。しかし、投資信託などの運用に限っては、なぜか過去の運用成績（トラックレコードと呼ばれます）が非常に重視されます。株式投資信託を考えれば簡単に分かるように、保有している株式の過去のパフォーマンスが良かったからこそ、その投資信託の過去のパフォーマンスが良いわけで、投資信託の過去のパフォーマンスで購入するかしないかを決めることは、上がった株だから買う、ということとほぼ同義です。しかし、リスク資産運用の原則からいえば、過去の成果は決して将来の成果を保証するものではありません。そればかりか、「成功した」投資家の多くがいわゆる逆張り屋であることを考えると、むしろ「最近パフォーマンスが悪かった投資信託を買った方がよい」とさえ、言えるかもしれません。90年代は、必ずしもそうではなかったようですが。
確かに、株式の場合、ソニーやNTTドコモのように、今後儲かるとみんなが予想する会社の株価は高くなるのに対し、市場価格で売買されるのではなく、純資産で設定や解約が行われる投資信託（日本の多くの投資信託の多くはそうです）の場合、仮にグレートな運用担当者が運用するファンドでも、設定や解約はあくまでも一口当たり純資産つまり基準価額で行われます。つまり、将来の高いパフォーマンスが、安く買えるわけです。しかし、これは長くは続きません。こうした投資信託には人気があつまり、運用報酬によって利益をあげることが目的の運用会社は、そのうち信託報酬率を上げるでしょう。現に、アクティブ運用を行う投資信託の信託報酬は、過去10年随分上がったように思います。
さらに、過去のデータから将来を予測しようとする場合必ず「過去の結果はたまたまであった」可能性が必ず付きまといます。この場合、過去のデータは将来とは全く無関係でさえあります。イカサマのないサイコロを転がして2回同じ目が出たからといって、3回目も同じ目が出る確率は、1/6でしかないのと同じです。
まとめると、過去のデータは、どのように理論を駆使しても、過去でしかありません。将来の予測に使えるかどうかは、全くわからないのです。
９）ではどうする?
投資信託についていえば、投資家の皆様は過去のデータから将来が予言できると頭から信じるほどナイーブではなく、もっと賢く運用を考えておられるようです。ここ数年、運用担当者がみずから証券会社を回り、自分の運用哲学を投資家の皆様に説明して回る、ということが盛んです。これは、投資家の皆様が過去のデータよりも、運用担当者の考え方が自分にとってうなずけるものかどうかを重視しているためであるように思います。その昔、ある（あくまでも過去のパフォーマンス実績によれば?）グレートなファンドマネージャーが「素晴らしい投資戦略や銘柄選択の考え方は、3分間で、誰にでもわかるように、説明できるものだ。」といっておりました。ある意味、これは正しいと思います。運用担当者の話を聞くことが重要なのは、投資家自身が、納得して投資する、というだけでなく、納得できる運用戦略こそが成功のかぎだからでもあるのです。
Appendix： 数学付録
本文では、考え方を示す以上の算数は用いませんでした。ここでは、実際に計算ができるよう、数式を示します。
① 複利年率のトータルリターン
まず、トータルリターンとは「投資期間を固定し、その期中に発生したキャッシュフローはすべて元の資産に再投資したと仮定して、投資期間終了時に得られているはずのリターン」でした。一般的には、次のように表せます。
ただし、V0: 投資スタート時の資産価値、Vt: t年目期末の資産価値（キャッシュフロー落ち後）、CFt: t年目期末のキャッシュフロー、n: 投資期間（年）、 
: X1からXnまでの合計。これを、期首の投資金額当たりに直せば次のようになります。
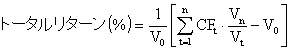
さらに複利年率のトータルリターンは次のようになります。
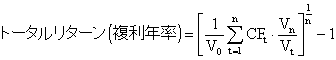
また、各期のリターンがわかっている場合、次のように表すことも出来ます。
ただし、
: X1からXnまでを掛け合わせたもの、rt: t期のリターン（%）。こうして計算したリターンは、金額加重平均収益率とも呼ばれます。
② 標準偏差
投資のリスクにはいろいろな定義がありえますが、最も使い勝手がよく、それでいて納得しやすい定義は「実現リターンが予想とどれぐらい大きく外れ得るか」というものだと思います。統計学ではこれを分散や標準偏差と呼ばれる指標で表します。分散は通常
で表し、次の式で計算できます。
i : それぞれの場合につけた通し番号、n: 場合の数、pi : それぞれの場合が起きる確率、ri: それぞれの場合が起きたときのリターン、
: 平均リターン。平均値からの差をとり、それを二乗することで、実現リターンの平均値からのブレを、プラスやマイナスの符号を取った大きさにし、それに確率を掛けています。絶対値をとったりせずに二乗して符号をはずす、というのは算数ではよく行われる方法です。分散は、「平均値からのブレの二乗の平均値」になっています。二乗がある分だけ、元の数と単位が違ってしまいます（この場合、元の数の単位は%、二乗しているから分散の単位は
）。これでは扱いにくいので、分散の平方根を取り、標準偏差σと呼びます。標準偏差は、「平均値からのブレの平均的な大きさ」と考えることが出来ます。パフォーマンス評価の文脈では、平均値は期待収益率、平均値からのブレはリスクですから、ブレの平均的な大きさが大きいほど、リスクが大きいということが出来ます。なお、本文で述べたようにリスク・リターンともに、往々にして過去のデータを用いて計算されます。過去のデータを使って分散や標準偏差を計算するときには、次の公式が用いられます。
分散：
標準偏差：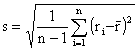
③ ベータ
システマティックリスク指標であるβ（ベータ）は、次の式で計算できます。
ただしCOV(x,y): xとyの共分散、px,y: xとyの相関係数、rm: 市場インデックスの期待（平均）リターン、σm: 市場インデックスの標準偏差、rp: 評価対象のポートフォリオや証券の期待（平均）リターン、σp: 評価対象のポートフォリオや証券の標準偏差。共分散は次のように計算します。
ただしi: それぞれの場合につけた通し番号、n: 場合の数、pi: それぞれの場合が起きる確率、ri: それぞれの場合が起きたときのリターン、 : 平均リターン。足文字のmは市場インデックスを、pは評価対象のポートフォリオや証券を表します。また、分散や標準偏差と同様、過去のデータを用いるなら、次のような式で共分散を計算します。
さらに、相関係数は次の式で得られます。
相関係数は、市場インデックスとポートフォリオや証券の連動性の指標です。一方、ポートフォリオの標準偏差/市場の標準偏差は、ポートフォリオのトータルリスクが市場のトータルリスクの何倍であるか、を表しています。両者を掛け合わせることで、ベータは市場が変動するとき、ポートフォリオがそれにつれてどれぐらいの大きさの変動を示すか、を表しています。
④ レジデュアルリスク
レジデュアルリターンは、単純にトータルリターンからシステマティックリターンを差し引いて残ったもの、という計算が出来ましたが、リスクについてはもう少しだけ複雑です。即ち、分散で考えると、レジデュアルリスク = トータルリスク － システマティックリスクが言えます。
ただし
: レジデュアルリスクの標準偏差（その二乗はレジデュアルリスクの分散）、σ: トータルリスクの標準偏差（同じくその二乗はトータルリスクの分散）、σm: 市場インデックスの標準偏差（同じくその二乗は市場インデックスの分散）。
しかし、標準偏差ではこれが成り立ちません。標準偏差は分散の二乗根ですから、レジデュアルリスクを標準偏差で表せば、次のような式になります。
筆者：P太郎（某大手運用会社勤務。専門はリスクマネジメント）
